ELEUSI - IL GIOCO PER ECCELLENZA
ELEUSIS - THE MARVELOUS GAME

REGOLE DEL GIOCO GAME RULES

LA LOGICA DEL GIOCO
Come nello scoprire le regole che governano l'universo reale, le Regole dell'Universo del gioco sono scoperte da una combinazione di ragionamenti induttivi.
Essi formano ipotesi basate su qualunque prova sia disponibile.
Inizialmente, senza informazioni a disposizione, le ipotesi sono poco più di tentativi casuali.
Ma, qualunque ipotesi casuale sia scelta, uno o più pezzi vengono messi sul tavolo.
Sia le giocate corrette che quelle scorrette sono informative e, come nella scienza reale, le ipotesi non possono essere provate come vere, ma possono essere falsificate con certezza.
Man mano che le giocate si susseguono emerge un pattern che permette di ipotizzare la Regola dell'Universo basandosi sia sulle giocate corrette che su quelle scorrette.
Più ipotesi possono essere rigettate sulla base delle giocate precedenti.

I PEZZI DEL GIOCO
Il gioco classico utilizza normali mazzi di carte.
Analizziamo le caratteristiche delle carte sulla base delle quali si definisce la Regola dell'Universo:



Per ogni caratteristrica abbiamo funzioni elementari:

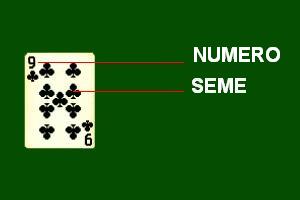
SEME COLORE(SEME)= {'ROSSO', 'NERO'}
TIPO(SEME)= {'CUORI', 'QUADRI', 'FIORI', 'PICCHE'}
SPIGOLOSO(SEME)= {'SI', 'NO'}
NUMERO VALORE(NUMERO) = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13}
TIPO(VALORE)= {'NORMALE', 'MASSIMO', 'MINIMO', 'MEDIO'}

Possiamo anche avere funzioni di funzioni, per esempio:
COLORE(SEME) INVERSO(COLORE(SEME))= {'NERO', 'ROSSO'}
VALORE(NUMERO) MODULO(VALORE(NUMERO), 2) = {'PARI', 'DISPARI'}
IMMAGINE(VALORE(NUMERO))= {'FIGURA', 'NON FIGURA'}

La regola combina queste funzioni per generare la sequenza. Il criterio è per confronto tra una carta e la precedente o gruppi di carte precedenti.
La sequenza di carte alternate per colore può così essere descritta:
INVERSO(COLORE(SEME)) del precedente
Si possono combinare funzioni che insistono su caratteristiche differenti:
se precedente COLORE(SEME)= 'ROSSO' metti MODULO(VALORE(NUMERO), 2) = 'PARI' altrimenti MODULO(VALORE(NUMERO), 2) = 'DISPARI'
Basta correggere di poco la regola precedente, per rendere quasi impossibile la soluzione:
se precedente COLORE(SEME)= 'ROSSO' metti MODULO(VALORE(NUMERO), 2) = 'PARI'

Il sito LUDOPATH di Ulrich Roth propone un mazzo di 192 carte con personaggi famosi così concepito:



In questo caso abbiamo a disposizione le seguenti funzioni elementari:

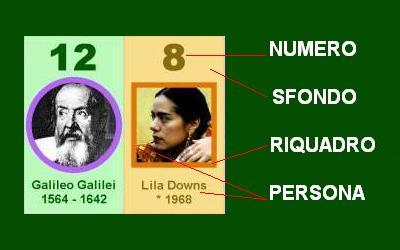
NUMERO VALORE(NUMERO) = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
TIPO(VALORE)= {'NORMALE, 'MASSIMO', 'MINIMO'}
SFONDO COLORE(SFONDO)= {'GIALLO', 'ROSA', 'VERDE', 'VIOLETTO'}
RIQUADRO COLORE(RIQUADRO)= {'VIOLA', 'ARANCIO', 'TURCHESE'}
FORMA(RIQUADRO)= {'QUADRATO', 'CERCHIO'}
PERSONA STATO(PERSONA)= {'VIVO', 'MORTO'}
SESSO(PERSONA)= {'MASCHIO', 'FEMMINA'}
PROFESSIONE(PERSONA)= { varie }

Anche in questo caso sono possibili le funzioni di funzioni, per esempio:
VALORE(NUMERO) MODULO(VALORE(NUMERO), 2) = {'PARI', 'DISPARI'}
FORMA(RIQUADRO) LATI(FORMA(RIQUADRO) = {0, 4}


NON CI SONO SOLTANTO LE CARTE
E' possibile pensare ad altri oggetti al posto delle carte. In un primo momento ho immaginato di usare figurini ferroviari, ma concettualmente non saremmo molto distanti dalle carte.
In più ci sarebbero un sacco di vincoli, per esempio se il treno che segue da una parte rispetta la regola 'LOCO CON DUE RIMORCHI PER COLORE', d'altra parte si tratta di un treno impossibile:



Bisognerebbe limitarsi per esempio ai soli carri merci, come quelli americani caratterizzati dal tipo e dalla compagnia di appartenenza.
Anche in questo caso i treni con tipi misti di carri sarebbero poco realistici.

Meglio è allora pensare a delle semplici pedine recanti un simbolo.
Ci si può sbizzarrire sui simboli da impiegare, per esempio i segni dello zodiaco e i pianeti, o le rune o alfabeti e cifre strane ecc.
Ho preferito proporre invece delle semplici figure geometriche; potete scaricare l'immagine che segue e stamparne quante copie volete.
Si possono incollare sulle pedine della dama o della tombola. Le stesse pedine possono riportare anche i simboli di conteggio e di profeta.



In questo caso, i simboli hanno una sola caratteristica, la forma. Le funzioni sono allora le serguenti:

FORMA COLORE(FORMA)= {'GIALLO', 'VERDE', 'ROSSO', 'BLU'}
LATI(FORMA)= {1, 2, 3, 4, 5, 6}
SPIGOLI(FORMA)= {0, 2, 3, 4, 5, 6}
REGOLARE(FORMA)= {'SI', 'NO'}
PRESENZACURVE(FORMA)= {'SI', 'NO'}

Anche in questo caso possiamo avere funzioni di funzioni, per esempio:
LATI(FORMA) MODULO(LATI(FORMA), 2)= {'PARI', 'DISPARI'}
COLORE(FORMA) TIPO(COLORE(FORMA))= {'BASE', 'COMPOSTO'}
TONO(COLORE(FORMA))= {'CHIARO', 'SCURO'}


La differenza sostanziale rispetto alle carte descritte sopra è che questi pezzi non hanno un numero associato.
Sarà quindi la REGOLA a contenere legami numerici. Vediamo qualche esempio

1. quattro simboli per colore


2. progressione con cambio simbolo (notare che la sequenza fino all'ultimo simbolo risponde anche alla regola: due simboli per colore)


3. simbolo con lato pari seguito da simbolo con lato dispari


4. simbolo differente dal precedente per forma e colore


5. due simboli rossi seguiti da un simbolo qualsiasi (quasi impossibile identificarla)


6. due simboli rossi seguiti da un simbolo qualsiasi di altro colore (la regola è leggermente diversa dalla precedente, ma molto più individuabile)



Si noti infine che dalla terza serie in poi la sequenza delle forme geometriche è sempre la stessa.
BUON DIVERTIMENTO!